728x90

재귀
- 어떤 사건이 자기 자신을 포함하고 다시 자기 자신을 사용하여 정의될 때 재귀적(recursive)이라고 함
- 이게 안되면 디바이드 앤 컨커, 다이나믹 프로그래밍 다 안됨
- 재귀호출: 자기 자신과 똑같은 메서드를 호출
- 선언적 프로그래밍(declarative programming) = 목적만 설정해 주면 중간 과정은 컴퓨터가 알아서 함
: 언제 종료하고, 이 문제를 어떤 식으로 정의 할 수 있는가 명시
직접(direct) 재귀: 자신과 같은 메서드 호출
간접(indirect) 재귀: 메서드 a가 메서드 b를 호출, 다시 메서드 b가 메서드 a를 호출
재귀함수를 짜는 법
1. 종료 조건
2. 문제의 정의
팩토리얼
- 음이 아닌 정수의 팩토리얼
1. 0! = 1
2. n > 0 이면 n! = n * (n-1)!
재귀 메서드 호출
static int factorial(int n) {
if(n > 0) {
return n * factorial(n-1); //n * (n-1)!
} else {
return 1; // 0! = 1
}
}- 1 * factoral(0) = (1 * 1) 반환
- 2 * factoral(0) = (2 * 1) 반환
- 3 * factoral(0) = (3 * 2) 반환
반복문 사용
static int factorial(int n) {
int answer = 1;
while(n != 0) {
answer *= n;
n = n-1;
//한줄로 쓰면 answer *= n--;
}
return answer;
}유클리드 호제법
2023.04.25 - [Study/Data Structure&Algorithm] - [알고리즘] 유클리드 호제법 (Euclidean algorithm)
재귀 메서드 호출
static int gcd(int x, int y) {
if(y == 0) //더는 나누어 떨어지지 않을 때
return x;
else
return gcd(y, x%y);
}- y = 0 일 때 라는 것은 더는 나누어 떨어지지 않을 때, 최대공약수는 x
- y ≠ 0 일 때 gcd( y, x%y ) 사용하여 y=0 될 때까지 반복
반복문 사용
static int gcd(int x, int y) {
while(y != 0) {
int temp = y;
y = x % y;
x = temp;
}
return x;
}배열 a의 모든 요소의 최대공약수
static int gcd(int x, int y) {
if(y == 0) {
return x;
} else {
return gcd(y, x % y);
}
}
//1. 첫번째, 두번째 요소의 공약수를 구하고 나머지 반복
static int gcdArray(int[] a) {
int z = gcd(a[0], a[1]);
for(int i = 2; i < a.length; i++) { //처음부터 끝까지 반복
z = gcd(z, a[i]); //첫번째에 10나옴
}
return z;
}
//2. no = 요소 개수, 1, 2, n개일 때로 나눔
static int gcdArray(int a[], int start, int no) {
if (no == 1)
return a[start];
else if (no == 2)
return gcd(a[start], a[start + 1]);
else
return gcd(a[start], gcdArray(a, start + 1, no - 1));
}재귀 알고리즘 분석
package chap05_1;
import java.util.Scanner;
public class Recur {
//재귀 함수
static void recur(int n) {
if(n > 0) {
recur(n-1); //n보다 1작은 수
System.out.println(n); //n 그대로 반환
recur(n-2); //n보다 2작은 수
}
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
System.out.print("정수를 입력하세요: ");
int x = scan.nextInt();
recur(x);
}
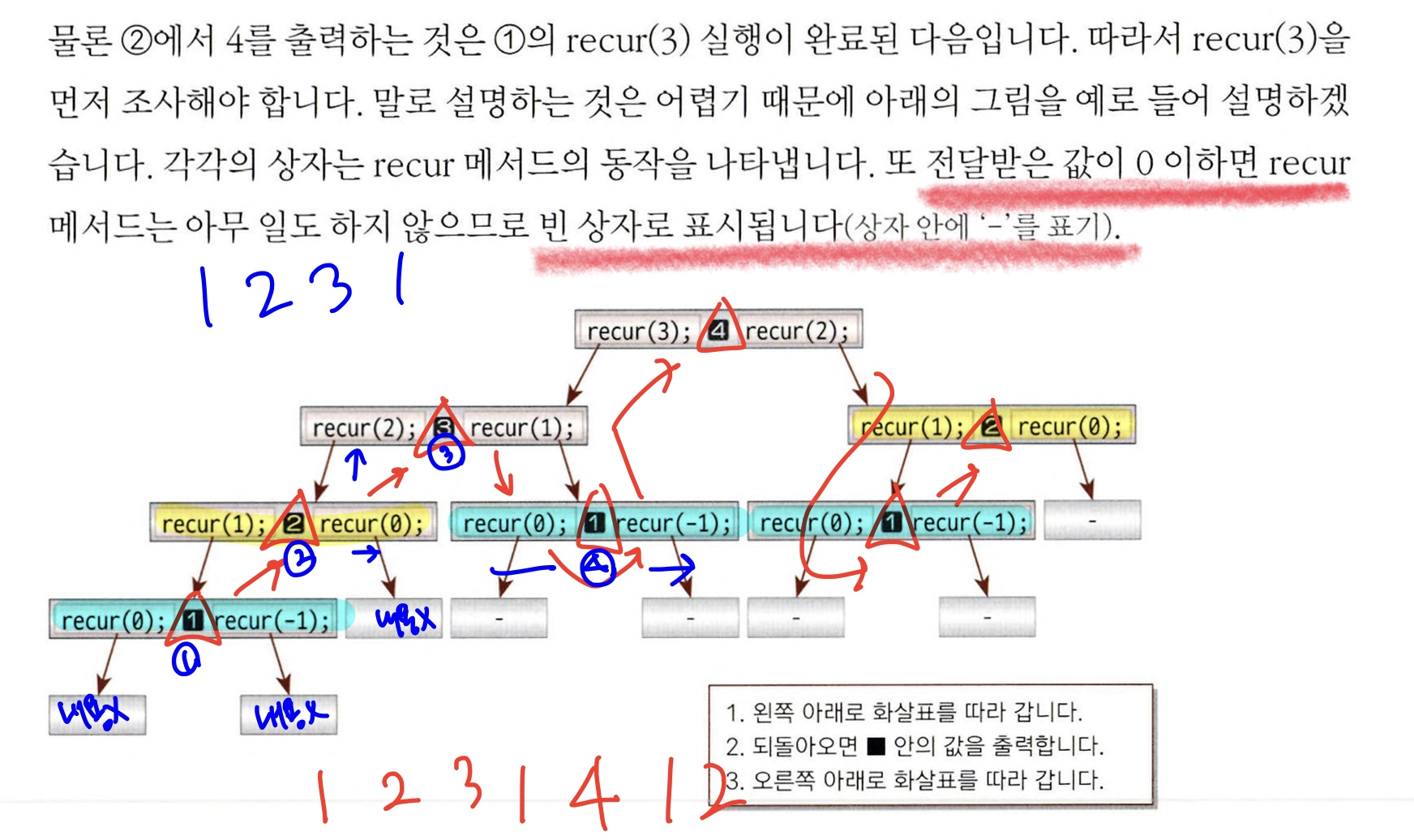
}하향식 (top down)
- 가장 위쪽에 위치한 상자의 메서드 호출부터 시작해 계단식으로 자세히 조사하는 분석 기법
- 위에서부터 내려오므로 recur(n-1) 부터 실행
- 같은 호출이 여러번 나올 수 있으므로 반드시 효율이 좋다고 할 수 없음
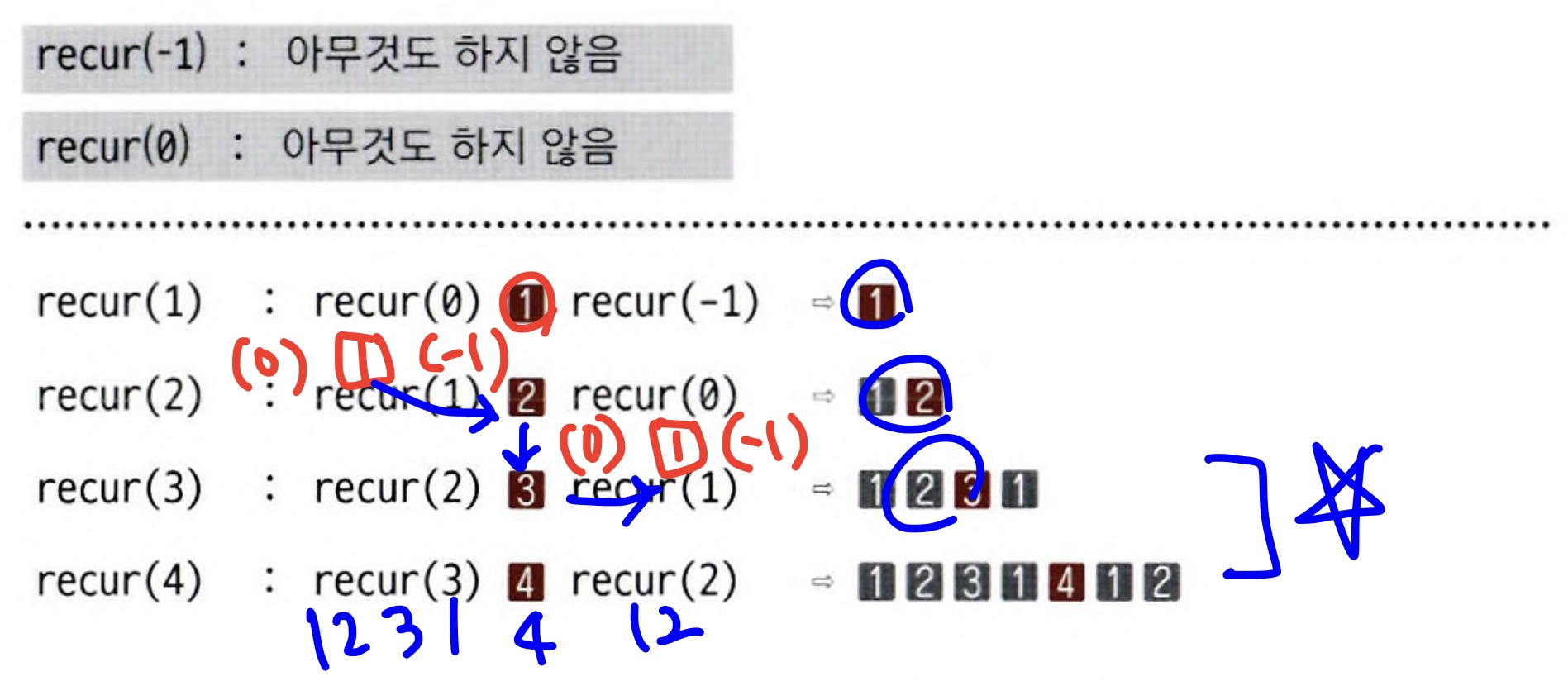
상향식 (down top)
- 아래쪽부터 쌓아 올리며 분석하는 방법
- recur 메서드는 n이 양수일 때만 실행하므로 recur(1)부터 수행
- recur(1) - recur(2) - recur(3) - recur(4)까지 쌓아 올리는 과정을 거치면 됨
recur2 메서드 (순서 중요)
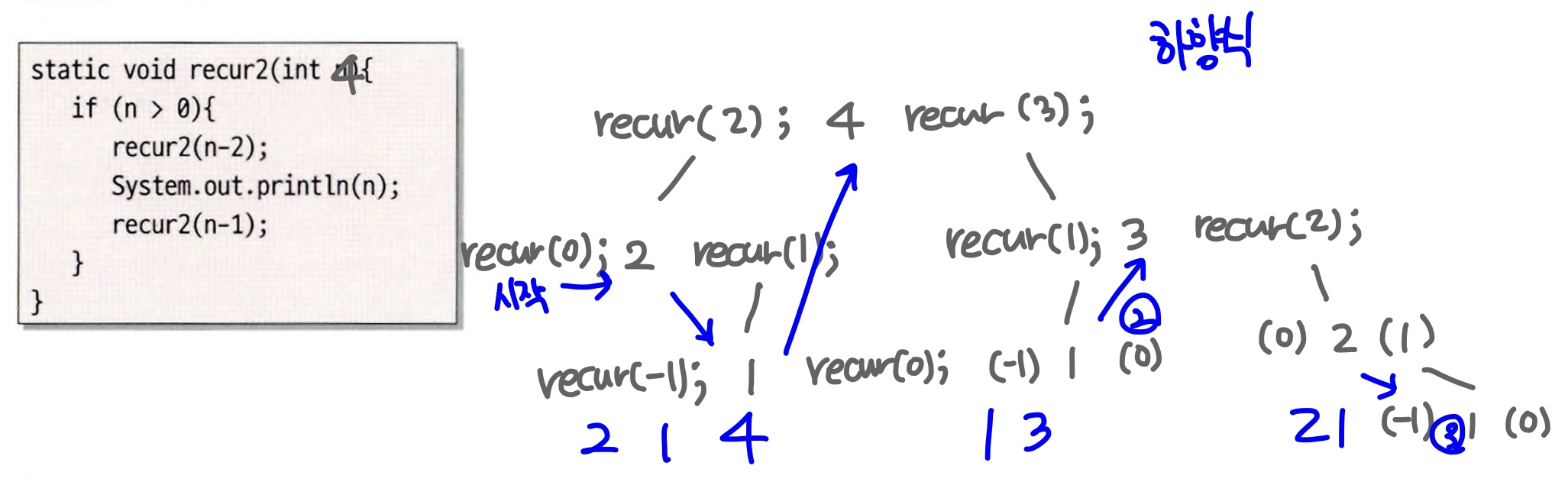

package chap05_1;
import java.util.Scanner;
public class Recur2 {
static void recur2(int n) {
if(n > 0) {
recur2(n-2);
System.out.println(n);
recur2(n-1);
}
//꼬리 재귀를 버린 코드
//while(n>0) {
// recur2(n-2);
// System.out.println(n);
// n=n-1;
//}
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
System.out.print("정수를 입력하세요: ");
int x = scan.nextInt();
recur2(x);
}
}비재귀적 표현
1. 꼬리 재귀의 제거
- recur(n-2) = 인자로 n-2를 전달하여 recur 메서드를 호출
n의 값을 n-2로 업데이트하고 메서드의 시작 지점으로 돌아감
//꼬리 재귀 제거
static void recur(int n) {
while(n > 0) {
recur(n-1);
System.out.println(n);
n = n-2;
}
}2. 재귀의 제거 (앞부분)
- 변수 n의 값을 호출하기 전에 recur(n-1)을 먼저 수행해야 함
- 예를 들어 n = 4일 때 재귀 호출 recur(3)의 처리가 완료하기 전 n의 값인 4를 저장해야 함
현재 n의 값을 '잠시' 저장한 후
저장했던 n을 다시 꺼내 그 값을 출력
▶ stack 사용
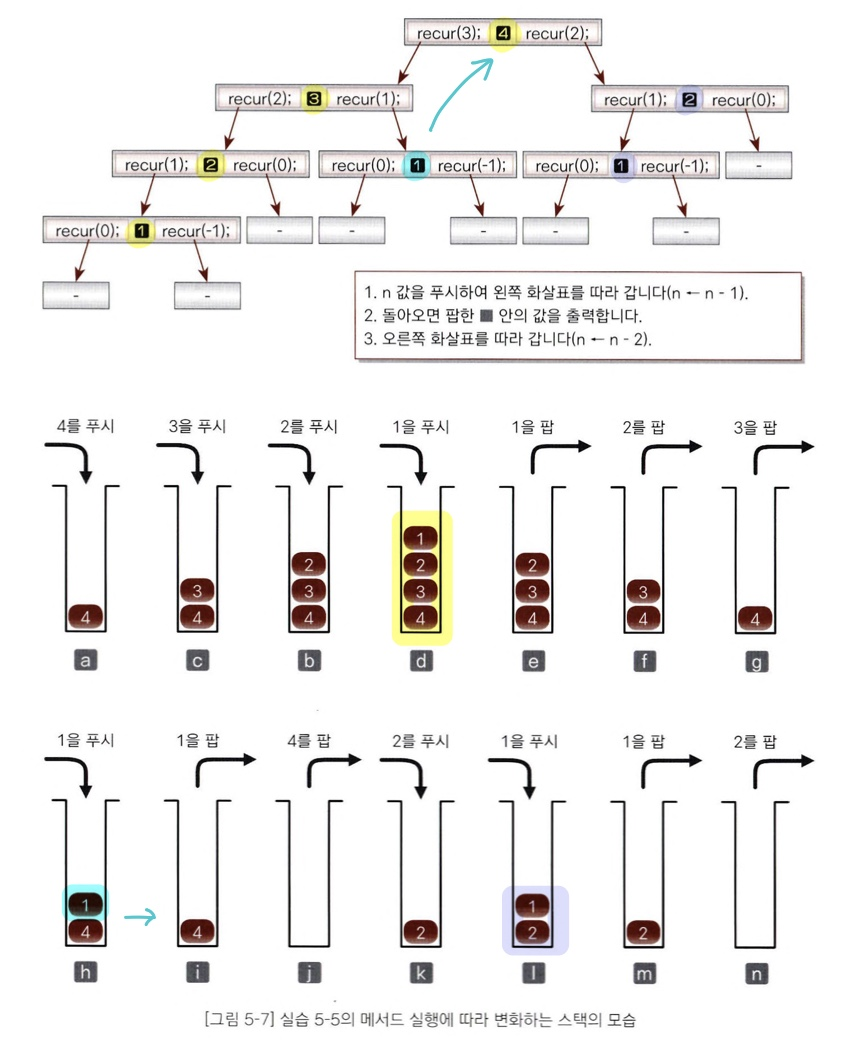
package chap05_1;
public class RecurX1 {
//재귀 제거
static void recur(int n) {
//정수 크기를 가진 stack 생성
IntStack s = new IntStack(n);
while(true) { //그림에서 가운데의 네모 숫자를 넣기 위함
if(n > 0) { //push
s.push(n); //n의 값을 푸시
n = n-1;
continue;
}
if(s.isEmpty() != true) { //pop, n < 0
n = s.pop();
System.out.println(n); //n의 값을 꺼내옴
n = n-2; //꼬리 재귀 제거
continue;
}
break;
}
}
}하노이의 탑
목표: 첫 번째 기둥의 모든 원반을 세 번째 기둥으로 최소의 횟수로 옮기는 것
1. 원반은 1개씩만 옮길 수 있음
2. 큰 원반을 작은 원반 위에 쌓을 수 없음
- 종료 조건 설정 - 원반이 1개 남았을 때 1번 원반(가장 작은 원)을 시작 기둥에서 목적 기둥으로 옮김
- 정의
- N개의 원반을 옮기기 위해 N-1개의 원반을 이웃 기둥으로 옮김
- 가장 큰 원반을 목적 기둥으로 옮김
- 이웃한 기둥에서 N-1개의 원반을 목적 기둥으로 옮김
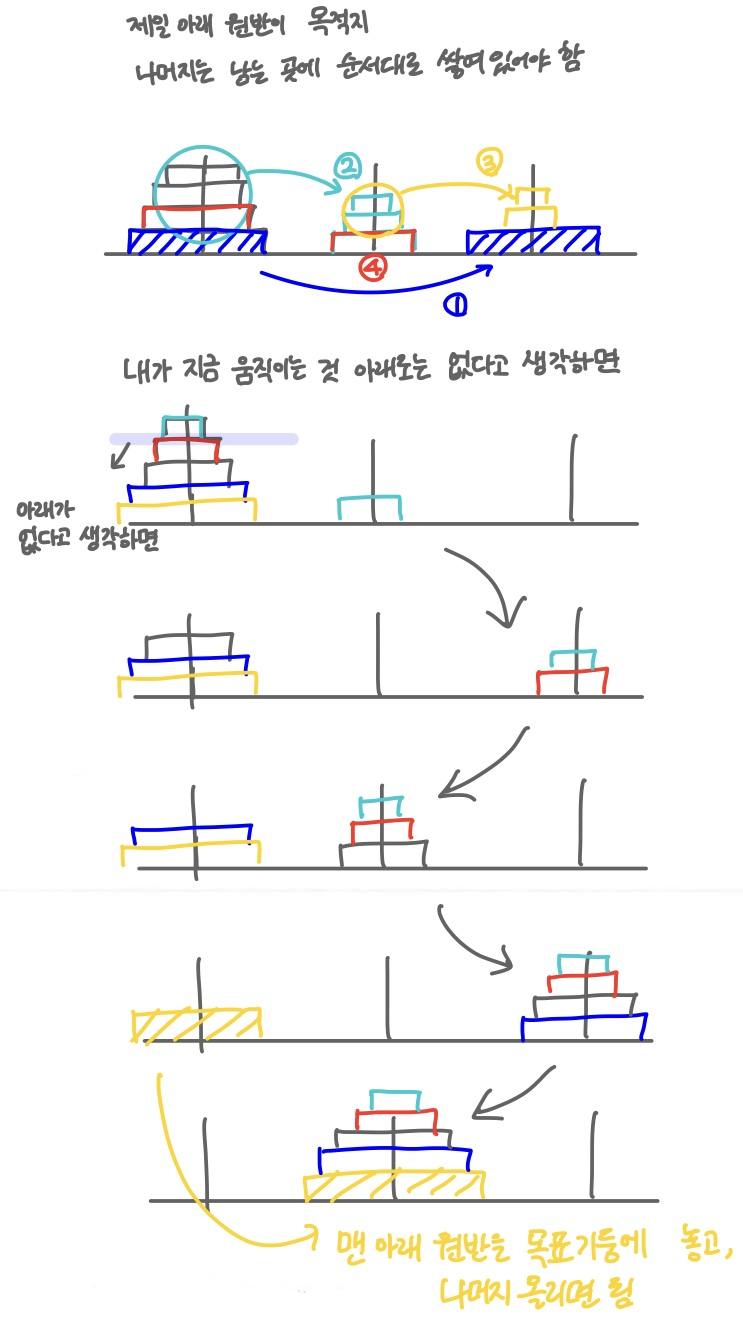
중간 기둥: 기둥 번호의 합 - 시작 기둥 - 목표 기둥
package chap05_3;
import java.util.Scanner;
//하노이의 탑
public class Hanoi {
//no개의 원반을 x번 기둥에서 y번 기둥으로 옮김
static void move(int no, int x, int y) {
if(no > 1) //시작 기둥의 값을 중간 기둥으로 옮김
//맨 아래 원반 제외하고 나머지들은 목적지가 아닌 곳으로 재귀적으로 이동시킴
move(no - 1, x, 6 - x - y); //기둥 번호의 합이 6이므로 중간 기둥 번호 = 6 - x - y
System.out.println("원반[" + no + "]을 " + x + "기둥에서 " + y + "기둥으로 옮김"); //시작 → 목표 기둥으로 옮김을 출력
if(no > 1) //중간 기둥의 값을 목표 기둥으로 옮김
//위에서 놨던 원반들을 목표기둥으로 옮김
move(no - 1 , 6 - x - y, y);
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
System.out.println("하노이의 탑");
System.out.print("원반의 개수: ");
int n = scan.nextInt();
move(n, 1, 3); //1번 기둥의 n개의 원반을 3번 기둥으로 옮김
}
}
콜라 문제
https://school.programmers.co.kr/learn/courses/30/lessons/132267
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
백트래킹 Backtracking
- 가능한 모든 경우를 시도하면서 조건에 맞지 않는 경우 빠르게 배제하여 해결책을 찾는 것
- 상태공간트리를 깊이우선탐색(DFS)으로 찾지만 해답이 없을 경우 하위트리를 방문하지 않고 부모 노드로 되돌아감
- 단계
1. 문제의 해를 구성하는 단계: 재귀적 호출
2. 조건 검사: 현재 상태가 조건을 만족하는지 확인
3. 백트래킹: 이전 상태로 돌아가 다른 선택 시도
void checkNode(Node v) {
Node u;
if (promising(v)) {
if (isSolution(v)) {
printSolution(v);
} else {
for (each child u of v) {
checkNode(u);
}
}
}
}- promising function 유망함수를 체크하는 것이 핵심
- 현재 조사중인 가지의 값에 대해 추적만 하면 됨
- 임의의 집합에서 기준에 따라 원소의 순서를 선택
8퀸 문제
- N*N 크기의 체스판에서 N개의 퀸을 서로 공격하지 않고(가로, 세로, 대각선) 배치하는 방법
- 유망 함수: 같은 열이나 같은 대각선에 놓이는지 확인
- 단순 일차원 배열로 풀 수 있음 ▶ 퀸을 배치한 상황(1, 3, 0, 2)
- 배열의 idx를 행번호, value를 열번호로 사용하면 됨
- 같은 열의 경우 일차원 배열의 value가 동일한 것이 있는지 확인
- 대각선의 경우 기울기의 개념 사용
abs(idx1 - idx2) == abs(arr[idx1] - arr[idx2])
def n_queens (i, col): //i는 depth, col은 열
n = len(col) - 1 //0부터 시작
if(promising(i, col)):
if(i == n): //depth가 n과 같다는 것은 끝까지 갔음을 의미
print(col[1: n + 1]) //col 1~n+1까지 출력 = 해당하는 col의 row 번호를 줌
else:
for(j in range(1, n + 1)): //모든 j에 대해서 체크 해 봐야함
col[i + 1] = j //첫번째 행, 두번째 행 ...
n_queens(i + 1, col) //재귀호출, depth 깊어짐def promising(i, col):
k = 1
flag = true
while(k < i and flag):
if(col[i] == col[k] or abs(col[i] - col[k]) == (i - k)): //같은 행에 있느냐? 대각선에 있느냐?
flag = False
k += 1
return flag- 혹은 java 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/12952
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
피로도 - 완전탐색
https://school.programmers.co.kr/learn/courses/30/lessons/87946#
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
728x90
'Study > Data Structure&Algorithm' 카테고리의 다른 글
| [자료구조&알고리즘] 리스트 (선형, 연결(포인터, 커서), 원형, 이중 연결) (0) | 2023.06.07 |
|---|---|
| [자료구조&알고리즘] 셸, 퀵, 병합, 힙, 도수(계수) 정렬 (0) | 2023.06.02 |
| [자료구조&알고리즘] stack(스택), queue(큐) (0) | 2023.05.07 |
| [알고리즘] 유클리드 호제법 (Euclidean algorithm), 약수, 배수 (0) | 2023.04.25 |
| [자료구조&알고리즘] 검색(검색 알고리즘, 선형검색, 이진검색) (0) | 2023.04.25 |
